高等演算法-度量設施選址問題 (Metric Facility Location) + 查看更多
一個商業決策:如何在眾多可能的地點中,選擇開設服務設施 (例如:倉庫、分店) 的位置,來最小化總成本?
1. 問題的基本設定 (Given)
設施集合 F (Facilities): 一堆潛在可以蓋設施的地點。
城市集合 C (Cities): 一堆需要服務的客戶或城市。
2. 相關成本 (Costs)
有兩種主要的成本:
開設成本 fi (Opening Cost):
這是指如果你決定在潛在地點 i ∈ F 蓋一個設施,你需要支付的固定成本。
連接成本 cij (Connection Cost):
這是指從城市 j 連接到設施 i 所需的成本。
在這個問題中,連接成本通常就是兩點之間的距離 (distance)。
3. 決策與目標 (The Problem)
你的決策是要找到兩樣東西,讓總成本最小化:
要開設的設施子集 I ⊆ F (Subset of Facilities to Open): 決定要在哪些地點 I 實際開設設施。
連接函數 ∅: C → I (Connection Function): 決定每個城市 j ∈ C 應該連接到哪一個已經開設的設施 ∅(j) ∈ I。
4. 最小化的總成本函數 (The Objective)
總成本由兩部分組成,目標是讓它們的總和最小:
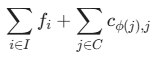
第一部分
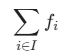 : 所有被開設設施的總開設成本。(你選了 I 裡面的哪些設施,就計算那些設施的 fi 總和。)
: 所有被開設設施的總開設成本。(你選了 I 裡面的哪些設施,就計算那些設施的 fi 總和。)第二部分
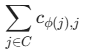 : 所有城市連接到它們所選設施的總連接成本。(每個城市 j 連接到它被分配到的設施 ∅(j),計算這個連接距離的總和。)
: 所有城市連接到它們所選設施的總連接成本。(每個城市 j 連接到它被分配到的設施 ∅(j),計算這個連接距離的總和。)
5. 【解釋說明】(Interpretation)
I: The set of facilities to open:哪些設施是活著的、有營運的。
∅ : indicating which facility city j connects to:每個客戶 j 會被指派給最近(或連接成本最低)的活著的設施。
The connection costs satisfy the triangle inequality. (連接成本滿足三角不等式):
這是「度量 (Metric)」這個詞的來源,它是一個關鍵限制。
三角不等式: 兩點之間,直線距離永遠最短。如果你從城市 A 經過一個中繼點 B 再到城市 C,這段距離不會比 A 直接到 C 的距離更短。在最佳化問題中,這保證了距離的合理性,避免了繞路的荒謬解。






